Komponen Simetris

Haloo sobat - sobat semua, kali ini ane akan bebrbagi sdikit ilmu yang ane punya. Kali ini ane menulis artikel tentang teknik Elektro. Sesuai dengan judulnya kalau ane akan membicarakan tentang Komponen Simetris.
Banyak sobat - sobat saya dan adek - adek junior yang binggung tentang komponen Simetris. Sebenarnya apa komponen Simetris??

Komponen Simetris adalah komponen yang terdapat pada setiap Arus, Tegangan dan parameter lainnya pada Tenaga Listrik apabila terjadi gangguan tidak simetris pada sebuah jaringan Sistem Tenaga Listrik.

Langsung kita membahas Komponen Simetris Lebih Dalam Lagi.......

-->

Pada tahun 1918 salah satu cara yang paling ampuh untuk menangani rangkaian fasamajemuk (poly-phase = berfasa banyak) tak seimbang telah dibahas C.L. Fortescue di hadapan suatu sidang American Institute of Electrical Engineers. Sejak saat itu, metode komponen simetris menjadi sangat penting dan merupakan pokok pembahasan berbagai artikel dan penyelidikan uji coba. Gangguan tak simetris pada sistem transmisi, yang dapat terjadi karena hubungan singkat, impedansi antar saluran, impedansi dari satu atau dua saluran ke tanah, atau penghantar yang terbuka, dipelajari dengan metode komponen simetris ini.

            Karya Fortescue membuktikan bahwa suatu sistem tak seimbang yang terdiri dari n fasor yang berhubungan (related) dapat diuraikan menjadi n buah sistem dengan fasor seimbang yang dinamakan komponen-komponen simetris (symmetricalcomponents) dari fasor aslinya. n buah fasor pada setiap himpunan komponennya adalah sama panjang, dan sudut di antara fasor yang bersebelahan dalam himpunan itu sama besarnya. Meskipun metoda ini berlaku untuk setiap sistem fasa-majemuk tak seimbang, kita akan membatasi pembahasan kita pada sistem tiga-fasa saja. Menurut teorema Fortescue, tiga fasor tak seimbang dari sistem tiga-fasa dapat diuraikan menjadi tiga sistem fasor yang seimbang. Himpunan seimbang komponenitu adalah :

1. Komponen urutan-positif (positive sequence components) yang terdiri dari tiga fasor yang sama besarnya, terpisah satu dengan yang lain dalam fasa sebesar120°, dan mempunyai urutan fasa yang sama seperti fasor aslinya.

2. Komponen urutan-negatif yang terdiri dari tiga fasor yang sama besarnya, terpisah satu dengan yang lain dalam fasa sebesar 120°, dan mempunyai urutan fasa yang berlawanan dengan fasor aslinya.

3. Komponen urutan nol yang terdiri dari tiga fasor yang sama besarnya dan dengan penggeseran fasa nol antara fasor yang satu dengan yang lain.

Telah menjadi kebiasaan umum, ketika memecahkan permasalahan dengan menggunakan komponen simetris bahwa ketiga fasa dari sistem dinyatakan sebagai a, b, dan c dengan cara yang demikian sehingga urutan fasa tegangan dan arus dalam sistem adalah abc. Jadi, urutan fasa komponen urutan positif dari fasor tak seimbang itu adalah abc, sedangkan urutan fasa dari komponen urutan negatifadalah acb. Jika fasor aslinya adalah tegangan, maka tegangan tersebut dapat dinyatakan dengan Va, Vb, dan Vc. Ketiga himpunan komponen simetris dinyatakan dengan subskrip tambahan 1 untuk komponen urutan-positif, 2 untuk komponen urutan negatif, dan 0 untuk komponen urutan nol. Komponen urutan positif dari Va,Vb dan Vc adalah Va1, Vb1, dan Vc1. Demikian pula, komponen urutan negatif adalah Va2, Vb2, dan Vc2, sedangkan komponen urutan nol adalah Va0, Vb0, dan Vc0.

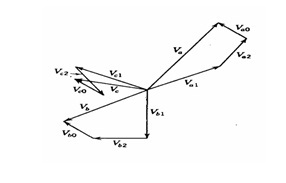
 Gambar dibawah. menunjukkan tiga himpunan komponen simetris semacam itu. Fasor arus akan dinyatakan dengan subskrip seperti untuk tegangan tersebut. Karena setiap fasor tak seimbang, yang asli adalah jumlah komponen, fasor asli yang dinyatakan dalam suku-suku komponennya adalah :

Va = Va1 + Va2  + Va0 (a)

Vb = Vb1 + Vb2 + Vb0 (b)

Vc =  Vc1 + Vc2 + Vc0 (c)

            Sintesis himpunan tiga fasor tak seimbang dari ketiga himpunan komponen simetris dalam Gambar dibawah.

-->

Karena adanya pergeseran fasa pada komponen simetris tegangan dan arus dalam sistem tiga-fasa, akan sangat memudahkan bila kita mempunyai metoda penulisan cepat untuk menunjukkan perputaran fasor dengan 120°. Hasil-kali dua buahbilangan kompleks adalah hasil-kali besarannya dan jumlah sudut fasanya. Jikabilangan kompleks yang menyatakan fasor dikalikan dengan bilangan kompleks yang besarnya satu dan sudutnya vi, bilangan kompleks yang dihasilkan adalah fasor yang sama besar dengan fasor aslinya tetapi fasanya tergeser dengan sudut vi.memutar fasor yang dikenakannya melalui sudut vi.

Kita sudah kenal dengan operator j, yang menyebabkan perputaran sebesar 90°, danoperator -1, yang menyebabkan perputaran sebesar 180°. Penggunaan operator j sebanyak dua kali berturut-turut akan menyebabkan perputaran melalui 90° + 90°,yang membawa kita pada kesimpulan bahwa j x j menyebabkan perputaran sebesar180°, dan karena itu kita ingat kembali bahwa j2 adalah sama dengan -1. Pangkat - pangkat yang lain dari operator j dapat diperoleh dengan analisis yang serupa. Huruf a biasanya digunakan untuk menunjukkan operator yang menyebabkan perputaran sebesar 120° dalam arah yang berlawanan dengan arah jarum jam.Operator semacam ini adalah bilangan kompleks yang besarnya satu dan sudutnya120° dan didefinisikan sebagai :

Gambar diabwah memperlihatkan fasor yang melukiskan berbagai pangkat dari a.

-->

Telah kita lihat pada Gambar diatas sintesis tiga fasor tak simetris dari tiga himpunan fasor simetris. Sintesis itu telah dilakukan sesuai dengan Persamaan (a) sampai dengan

 (b). Sekarang marilah kita periksa persamaan tersebut untuk menentukan bagaimana menguraikan ketiga fasor tak simetris itu menjadi komponen simetrisnya. Mula-mula, kita perhatikan bahwa banyaknya kuantitas yang diketahui dapat dikurangi dengan menyatakan masing-masing komponen Vb dan Vc sebagai hasil kali fungsi operator a dan komponen Va. Dengan berpedoman pada Gambar fasor seimbang,hubungan berikut dapat diperiksa kebenarannya: Persamaan (d).

           

                            

yang menunjukkan pada kita bagaimana menguraikan tiga fasor tak simetris menjadi komponen simetrisnya. Hubungan ini demikian pentingnya sehingga kita dapat menulis masing-masing persamaan itu dalam bentuk yang biasa. Dari Persamaan(k), kita peroleh:

                                            

Jika diperlukan, komponen Vb0, Vb1, Vb2, Vc0, Vc1, dan Vc2, dapat diperoleh persamaan (d).

Persamaan (n) menunjukkan bahwa tidak akan ada komponen urutan-nol jika jumlah fasor tak seimbang itu sama dengan nol. Karena jumlah fasor tegangan antar saluran pada sistem tiga-fasa selalu nol, maka komponen urutan-nol tidak pernah terdapat dalam tegangan saluran itu, tanpa memandang besarnya ketidak seimbangannya. Jumlah ketiga fasor tegangan saluran ke netral tidak selalu harus sama dengan nol, dan tegangan ke netral dapat mengandung komponen urutan-nol.

Persamaan yang terdahulu sebenarnya dapat pula ditulis untuk setiap himpunan fasor yang berhubungan, dan kita dapat pula menuliskannya untuk arus sebagai ganti tegangan. Persamaan tersebut dapat diselesaikan baik secara analitis maupun secara grafis. Karena beberapa persamaan yang terdahulu sangat mendasar, marilah kita tuliskan ringkasannya untuk arus-arus:

            Ia = Ia1 + Ia2  + Ia0 ……………………………………… ( o )

            Ib = Ib1 + Ib2 + Ib0 ……………………………………… ( p )

            Ic =  Ic1 + Ic2 + Ic0………………………………………  ( q )

       

Jika tidak ada jalur yang melalui netral dari sistem tiga-fasa, In, adalah nol, dan arus saluran tidak mengandung komponen urutan-nol. Suatu beban dengan hubungan Delta  tidak menyediakan jalur ke netral, dan karena itu arus saluran yang mengalir ke beban yang dihubungkanDelta  tidak dapat mengandung komponen urutan-nol.
Untuk mendapatkan File Word (.docx), Sobat sobat dapat download di sini 

Terimakasih Telah berkunjung ke Arie Star Light, Tinggalkan jejak sobat - sobat berupa like dan G+1